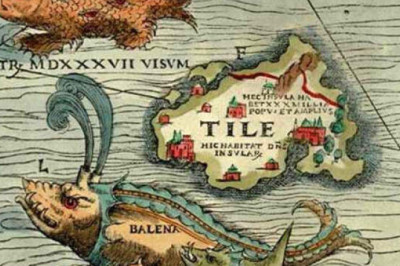
Египетские числовые обозначения
Десятичная система счета в Древнем Египте сложилась на основе использования для подсчета предметов количества пальцев на обеих руках. Числа от одного до девяти обозначались соответствующим количеством черточек, для десятков, сотен, тысяч и так далее существовали особые иероглифические знаки.
Вероятнее всего, цифровые египетские символы возникли как результат созвучия того или иного числительного и названия какого-либо предмета, ведь в эпоху становления письменности знаки-пиктограммы имели строго предметное значение. Так, например, сотни обозначались иероглифом, изображающим веревку, десятки тысяч – изображением пальца.
В эпоху Среднего царства (начало II тысячелетия до н. э.) появляется более упрощенная, удобная для письма на папирусе иератическая форма письменности, соответствующим образом меняется и написание цифровых знаков. Знаменитые математические папирусы написаны иератическим письмом. Иероглифика применялась в основном для настенных надписей.
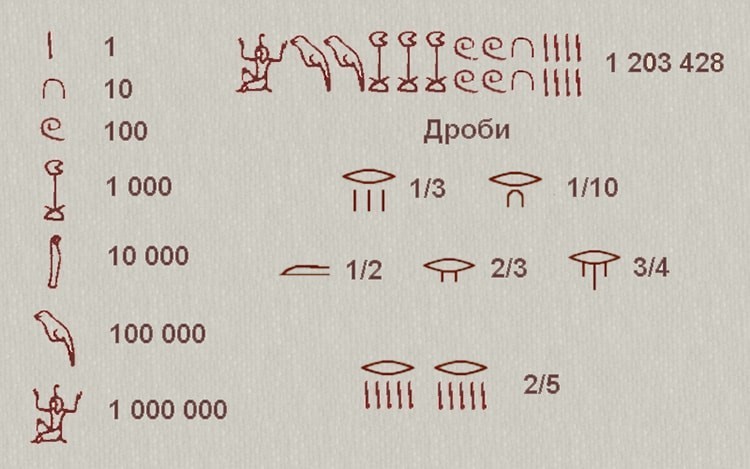
Система древнеегипетской нумерации не менялась на протяжении тысяч лет. Позиционного способа записи чисел древние египтяне не знали, поскольку не подошли еще к понятию нуля не только как самостоятельной величины, но и просто как отсутствия количества в определенном разряде (этой начальной ступени достигла математика в Вавилоне).
Дроби в математике Древнего Египта
Египтяне имели понятие о дробях и умели производить некоторые операции с дробными числами. Египетские дроби представляют собой числа вида 1/n (так называемые аликвотные дроби), поскольку дробь представлялась египтянами как одна часть чего-либо. Исключением являются дроби 2/3 и 3/4. Неотъемлемым элементом записи дробного числа был иероглиф, переводимый обычно как «один из (некоторого количества)». Для наиболее употребительных дробей существовали особые знаки.
Дробь, числитель которой отличен от единицы, египетский писец понимал буквально, как несколько частей какого-либо числа, и буквально же записывал. Например, дважды подряд 1/5, если требовалось изобразить число 2/5. Так что египетская система дробей была весьма громоздка.
Интересно, что один из священных символов египтян – так называемое «око Хора» – также имеет математический смысл. Один из вариантов мифа о схватке между божеством ярости и разрушения Сетом и его племянником солнечным богом Хором гласит, что Сет выбил Хору левый глаз и разорвал или растоптал его. Боги восстановили глаз, но не полностью. Око Хора олицетворяло разные аспекты божественного порядка в мироустройстве, такие как идея плодородия или власть фараона.
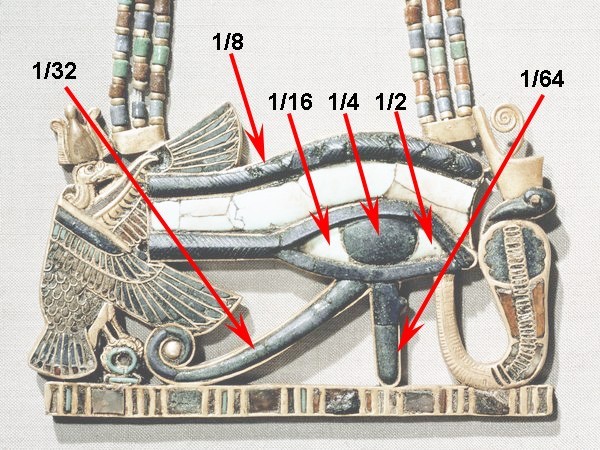
Изображение ока, почитавшегося как амулет, содержит элементы, обозначающие особый ряд чисел. Это дроби, каждая из которых вдвое меньше предыдущей: 1/2, 1/4, 1/8, 1/16, 1/32 и 1/64. Символ божественного глаза, таким образом, представляет их сумму – 63/64. Некоторые историки-математики полагают, что в этом символе отражено понятие египтян о геометрической прогрессии. Составные части изображения ока Хора использовались в практических расчетах, например при измерении объема сыпучих веществ, таких как зерно.
Принципы арифметических действий
Метод, которым пользовались египтяне при выполнении простейших арифметических операций, состоял в подсчете итогового количества символов, обозначающих разряды чисел. Единицы складывались с единицами, десятки с десятками и так далее, после чего производилась окончательная запись результата. Если при суммировании получалось более десяти знаков в каком-либо разряде, «лишний» десяток переходил в высший разряд и записывался соответствующим иероглифом. Вычитание производилось таким же способом.
Без применения таблицы умножения, которой египтяне не знали, процесс вычисления произведения двух чисел, особенно многозначных, был чрезвычайно громоздким. Как правило, египтяне пользовались методом последовательного удвоения. Один из множителей раскладывался на сумму чисел, которые мы сегодня назвали бы степенями двух. Для египтянина это означало количество последовательных удвоений второго множителя и итоговое суммирование результатов. Например, умножая 53 на 46, египетский писец разложил бы 46 на сумму 32 + 8 + 4 + 2 и составил бы табличку, которую вы можете видеть ниже.
Суммируя результаты в отмеченных строках, он получил бы 2438 – столько же, сколько и мы сегодня, но иным способом. Интересно, что такой двоичный метод умножения применяется в наше время в вычислительной технике.
Иногда, помимо удвоения, число могли умножать на десять (поскольку использовалась десятичная система) или на пять, как на половину десятки. Вот еще один пример на умножение с записью египетскими символами (косой черточкой помечались складываемые результаты).

Операция деления производилась также по принципу удвоения делителя. Искомое число при умножении на делитель должно было дать указанное в условии задачи делимое.
Математические знания и навыки египтян
Известно, что египтяне знали возведение в степень, а также применяли обратную операцию – извлечение квадратного корня. Кроме того, они имели представление о прогрессии и решали задачи, сводящиеся к уравнениям. Правда, уравнения как таковые не составлялись, так как еще не сложилось понимание того, что математические отношения между величинами носят универсальный характер. Задачи группировались по тематике: размежевание земель, распределение продуктов и так далее.
В условиях задач присутствует неизвестная величина, которую требуется найти. Она обозначается иероглифом «множество», «куча» и является аналогом величины «икс» в современной алгебре. Условия часто излагаются в форме, которая, казалось бы, просто требует составления и решения простейшего алгебраического уравнения, например: «куча» складывается с 1/4, также содержащей «кучу», и получается 15. Но египтянин не решал уравнение x + x/4 = 15, а подбирал искомую величину, которая удовлетворяла бы условиям.
Значительных успехов математика Древнего Египта достигла в решении геометрических задач, связанных с потребностями строительства и землемерных работ. О круге задач, которые стояли перед писцами, и о способах их решения мы знаем благодаря тому, что сохранилось несколько письменных памятников на папирусе, содержащих примеры вычислений.
Древнеегипетский задачник
Один из наиболее полных источников по истории математики в Египте – так называемый математический папирус Ринда (по имени первого владельца). Он хранится в Британском музее в виде двух частей. Небольшие фрагменты также есть в музее Нью-Йоркского исторического общества. Его также называют папирусом Ахмеса – по имени писца, переписавшего этот документ около 1650 года до н. э.
Папирус представляет собой сборник задач с решениями. Всего он содержит более 80 математических примеров по арифметике и геометрии. Например, задача на равное распределение между 10 работниками 9 хлебов решалась так: 7 хлебов делятся на 3 части каждый, и работникам выдается по 2/3 хлеба, при этом в остатке имеем 1/3. Два хлеба делятся на 5 частей каждый, выдается по 1/5 на человека. Оставшуюся треть хлеба делят на 10 частей.
Есть задача и на неравное распределение 10 мер зерна между 10 людьми. В результате образуется арифметическая прогрессия с разностью 1/8 меры.

Задача на геометрическую прогрессию носит шуточный характер: в 7 домах живет по 7 кошек, каждая из которых съела по 7 мышей. Каждая мышь съела 7 колосков, каждый колос приносит 7 мер хлеба. Нужно вычислить общее количество домов, кошек, мышей, колосьев и хлебных мер. Оно составляет 19607.
Геометрические задачи
Немалый интерес представляют математические примеры, демонстрирующие уровень знаний египтян в области геометрии. Это нахождение объема куба, площади трапеции, вычисление наклона пирамиды. Наклон выражался не в градусах, а рассчитывался как отношение половины основания пирамиды к ее высоте. Эта величина, аналогичная современному котангенсу, называлась «секед». Основными единицами длины служили локоть, составлявший 45 см («царский локоть» – 52,5 см) и хет – 100 локтей, основная единица площади – сешат, равный 100 квадратным локтям (около 0,28 Га).
Египтяне успешно справлялись с вычислением площадей треугольников, применяя способ, аналогичный современному. Вот задача из папируса Ринда: чему равна площадь треугольника, имеющего высоту 10 хет (1000 локтей) и основание 4 хета? В качестве решения предлагается десять умножить на половину от четырех. Мы видим, что метод решения абсолютно верный, подается в конкретном численном виде, а не в формализованном – умножить высоту на половину основания.
Весьма интересна задача на вычисление площади круга. Согласно приведенному решению, она равна величине 8/9 диаметра, возведенной в квадрат. Если теперь из полученной площади вычислить число «пи» (как отношение учетверенной площади к квадрату диаметра), то оно составит около 3,16, то есть довольно близко к истинной величине «пи». Таким образом, египетский способ решения площади круга был достаточно точным.
Московский папирус
Еще один важный источник наших знаний об уровне математики у древних египтян – Московский математический папирус (он же папирус Голенищева), хранящийся в Музее изобразительных искусств им. А. С. Пушкина. Это тоже задачник с решениями. Он не так обширен, содержит 25 задач, но имеет более древний возраст – примерно на 200 лет старше папируса Ринда. Большинство примеров в папирусе – геометрические, в том числе задача на вычисление площади корзины (то есть криволинейной поверхности).

В одной из задач приведен способ нахождения объема усеченной пирамиды, совершенно аналогичный современной формуле. Но поскольку все решения в египетских задачниках имеют «рецептурный» характер и приводятся без промежуточных логических этапов, без всякого объяснения, остается неизвестным, каким образом египтяне нашли эту формулу.
Астрономия, математика и календарь
Древнеегипетская математика связана и с календарными вычислениями, основанными на повторяемости некоторых астрономических явлений. Прежде всего, это предсказание ежегодного подъема Нила. Египетские жрецы заметили, что начало разлива реки на широте Мемфиса обычно совпадает с днем, когда на юге перед восходом Солнца становится виден Сириус (большую часть года эта звезда на данной широте не наблюдается).
Первоначально простейший сельскохозяйственный календарь не был привязан к астрономическим событиям и основывался на простом наблюдении сезонных изменений. Затем он получил точную привязку к восходу Сириуса, а вместе с ней появилась возможность уточнения и дальнейшего усложнения. Без математических навыков жрецы не могли бы уточнять календарь (впрочем, окончательно устранить недостатки календаря египтянам так и не удалось).

Не менее важным было умение выбрать благоприятные моменты для проведения тех или иных религиозных празднеств, также приуроченных к различным астрономическим феноменам. Так что развитие математики и астрономии в Древнем Египте, безусловно, связано с ведением календарных расчетов.
Кроме того, математические знания требуются для хронометрии при наблюдении звездного неба. Известно, что такими наблюдениями занималась особая группа жрецов – «распорядители часов».
Неотъемлемая часть ранней истории науки
При рассмотрении особенностей и уровня развития математики в Древнем Египте видна существенная незрелость, так и не преодоленная за три тысячи лет существования древнеегипетской цивилизации. До нас не дошли сколько-нибудь информативные источники эпохи становления математики, и мы не знаем, как оно происходило. Но ясно, что после некоторого развития уровень знаний и навыков застыл в «рецептурной», предметной форме без признаков прогресса на многие сотни лет.

По-видимому, устойчивый и однообразный круг вопросов, решаемых при помощи уже сложившихся методов, не создавал «спроса» на новые идеи в математике, которая и так справлялась с решением задач строительства, сельского хозяйства, налогообложения и распределения, примитивной торговли и обслуживания календаря и ранней астрономии. Кроме того, архаическое мышление не требует формирования строгой логической, доказательной базы – оно следует рецептуре как ритуалу, и это также сказалось на застойном характере древнеегипетской математики.
Вместе с тем необходимо заметить, что научное знание вообще и математика в частности делали еще первые шаги, а они всегда самые трудные. В примерах, которые демонстрируют нам папирусы с задачами, уже видны начальные ступени обобщения знаний – пока без попыток формализации. Можно сказать, что математика Древнего Египта в том виде, как мы ее знаем (из-за недостаточности источниковой базы по позднему периоду древнеегипетской истории) – это еще не наука в современном понимании, но самое начало пути к ней.